仅介绍公式进行运算，偶尔涉及部分推导便于理解，严格规范证明还是要看《初等数论》书。

不定方程

在扩展的欧几里得算法的推导中涉及了不定方程的相关方法，解方程还是挺有用的。

二元一次不定方程

$ax+by=c$

通解表示形式：$x=x_{0}-b_{1}t$，$y=y_{0}+a_{1}t$。其中$a_{1}=\frac{a}{gcd(a,b)}$，$b_{1}=\frac{b}{gcd(a,b)}$。
有解的充分必要条件$gcd(a,b)|c$。
求解过程：
先依据扩展欧几里得算法求出$ax+by=1$的解$x_{0}$和$y_{0}$。得到原方程的特解$x_{1}=c\cdot x_{0}$和$y_{1}=c\cdot y_{0}$。通解即由特解表示出来。

欧拉函数及其性质

就是求m的简化剩余系$\varphi (m)$。

① 若$m_{1}$和$m_{2}$是两个互质的正整数，则$\varphi (m_{1}m_{2})=\varphi (m_{1})\cdot \varphi (m_{2})$。

② 若$a=p_{1}^{\alpha_{1}}p_{2}^{\alpha_{2}}…p_{k}^{\alpha_{k}}$，则$\varphi (a)=a(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})…(1-\frac{1}{p_{k}})$。

推论：若$a=p^{k}$，则$\varphi (a)=p^{k}-p^{k-1}$

欧拉定理

若$gcd(a,m)=1$，则

$a^{\varphi (m)}\equiv 1(modm)$

费马小定理

若$p$是质数，则

$a^{p}\equiv a(modp)$

求逆元的两种方法

费马小定理

如果$p$是质数，则可以用上面的费马定理。$a^{p}\equiv a(modp)$，则$a^{p-1}\equiv 1(modp)$，即$a \cdot a^{p-2}\equiv 1(modp)$。
$a$关于$p$的逆元是$a^{p-2}$。

扩展的欧几里得算法

$a \cdot b\equiv 1(modn)$，即$ab+kn=1$，可以解出$b$和$k$。
具体过程：
$ax+by=1$，$gcd(a,b)=1=gcd(b, a\%b)=…$，一直继续下去得到解。
例如：$107x+37y=1$
$107=37×2+33$
$37=33×1+4$
$33=4×8+1$
回代
$1=33-4×8$
$=33-(37-33)×8$
$=(107-37×2)-[37-(107-37×2)]×8$
$=107×9-37×26$
得到解9和-26。

孙子定理

解同余式：

$\left\{\begin{matrix} x & \equiv & a_{1} & mod(m_{1})\\ x & \equiv & a_{2} & mod(m_{2})\\ ... & ... & & \\ x & \equiv & a_{n} & mod(m_{n}) \end{matrix}\right.$

解法：
设$m=m_{1}\cdot m_{2}\cdot …\cdot m_{n}$。$M_{i}=\frac{m}{m_{i}}$，i=1,2…n
解出$M_{i}$关于$m_{i}$的逆元$M_{i}^{‘}$。
则$x\equiv \sum_{i=1}^{n}(a_{i}\cdot M_{i}\cdot M_{i}^{‘})modm$

经典例题：今不知何物，三三数之剩二，五五数之剩三，七七数之剩二，问物几何。
化为同余式问题：

$\left\{\begin{matrix} x & \equiv & 2 & (mod3)\\ x & \equiv & 3 & (mod5)\\ x & \equiv & 2 & (mod7) \end{matrix}\right.$

解：$m=3×5×7=105$，$M_{1}=35$，$M_{2}=21$，$M_{3}=15$。

$35M_{1}^{‘}\equiv 1(mod3)$，$35-3×11=2$，$M_{1}^{‘}\equiv 2(mod3)$。

$21M_{2}^{‘}\equiv 1(mod5)$，$21-5×4=1$，$M_{2}^{‘}\equiv 1(mod5)$。

$15M_{3}^{‘}\equiv 1(mod7)$，$15-7×2=1$，$M_{3}^{‘}\equiv 1(mod7)$。

结果为：
$x\equiv 2×35×2+3×21×1+2×15×1=233(mod105)$

离散对数

$2^{x}\equiv 13(mod23)$
使用SageMath求解

1	x=discrete_log(mod(13,23),mod(2,23))

一些小运算技巧

弃九法——判断乘积是否正确的充分条件

由普通方法计算得到整数a，b的乘积P。令
$a=a_{n}10^{n}+a_{n-1}10^{n-1}+…+a_{0}$，

$b=b_{m}10^{m}+b_{m-1}10^{m-1}+…+b_{0}$,

$P=c_{l}10^{l}+c_{l-1}10^{l-1}+…+c_{0}$

若$(\sum_{i=0}^{n}a_{i})(\sum_{j=0}^{m}b_{j})\not\equiv \sum_{k=0}^{l}c_{k}(mod9)$，则求得的乘积P是错误的。

就是划掉加起来整除9的，剩下的就是余数。
注：只是充分不必要条件，如果验算失败则一定是错误的，但错误的乘积不一定验算失败。

例：a=28997，b=39495，普通乘法计算了一个P=1145236415。

a划掉2+7，两个9，剩下8。$a\equiv 8(mod9)$

b划掉4+5，两个9，剩下3。$b\equiv 3(mod9)$

P划掉两个4+5，3+6，剩下1+1+2+1=5，$P\equiv 5(mod9)$

由于$3\cdot 8\not\equiv 5(mod9)$，计算错误。

解同余式

一次同余式

$ax\equiv b(mod m)$化为不定方程求解。

方程组

$\left\{\begin{matrix} x & \equiv & a_{1} & mod(m_{1})\\ x & \equiv & a_{2} & mod(m_{2})\\ ... & ... & & \\ x & \equiv & a_{n} & mod(m_{n}) \end{matrix}\right.$

应用孙子定理。

高次同余式

一般同余式

若$m_{1}$，$m_{2}$，…，$m_{k}$是$k$个两两互质的正整数，且$m=m_{1}m_{2}…m_{k}$，则同余式$f(x)\equiv 0(mod m)$与同余式组$f(x)\equiv 0(mod m_{i})$等价。

例1：解同余式$31x^{4}+57x^{3}+96x+191\equiv 0(mod 225)$
$225=3^{2} \cdot 5^{2}$
解：
等价于解同余式方程组
$\left\{\begin{matrix}4x^{4} +3x^{3}+6x+2\equiv 0(mod 3^{2})
\\
6x^{4} +7x^{3}-4x-9\equiv 0(mod 5^{2})
\end{matrix}\right.$
1）先解$4x^{4} +3x^{3}+6x+2\equiv 0(mod 3)$
$x^{4} -1\equiv 0\left ( mod 3 \right ) $
$x\equiv \pm 1 \left ( mod 3 \right ) $
验证：
$f’\left ( x \right ) = 16x^{3} +9x^{2} +6$
$f’\left ( 1 \right ) =31$，$3 \nmid 31$。
$f’\left ( 1 \right ) =-1$，$3 \nmid -1$。

$x_{1} =3t_{1}+1$，$f\left ( 1+3t_{1} \right ) = f\left ( 1 \right ) +3t_{1}f’\left ( 1 \right )\equiv 0\left ( mod9 \right ) $
$15+93t_{1}\equiv 0\left ( mod9 \right ) $ （泰勒公式）
$5+31t_{1}\equiv 0\left ( mod3 \right ) $ （$am\equiv bm\left ( modqm \right ) $ => $a\equiv b\left ( modq \right ) $）
$2+t_{1}\equiv 0\left ( mod3 \right ) $
$t_{1}\equiv 1\left ( mod3 \right ) $
=> $x_{1}\equiv 1+3t_{1}\equiv 4\left ( mod3^{2} \right ) $

同理，$x_{2} =3t_{2}-1$，$f\left ( 3t_{2}-1 \right ) = f\left ( -1 \right ) +3t_{2}f’\left ( -1 \right )\equiv 0\left ( mod9 \right )$。
$f\left ( -1 \right ) +3t_{2}f\left ( -1 \right ) \equiv 0\left ( mod9 \right ) $
$-3-3t_{2}\equiv 0\left ( mod9 \right ) $
$-1-t_{2}\equiv 0\left ( mod3 \right ) $
$t_{2}\equiv 2\left ( mod3 \right ) $
=> $x_{2}\equiv 2t_{2}-1\equiv 5\left ( mod3^{2} \right ) $

2）再解$g(x)=6x^{4} +7x^{3}-4x-9\equiv 0(mod 5^{2})$
$x^{4}+2x^{3}+x+1\equiv 0\left ( mod5 \right ) $
验证0~4哪个符合，得到$x\equiv 1,2\left ( mod5 \right ) $
验证：
$g’(x)=24x^{3}+21x^{2}-4$
$g’(1)=41$，$5 \nmid 41$
$g’(2)=272$，$5 \nmid 272$

$x_{3} =5t_{3}+1$，$x_{4} =5t_{4}+2$
$g(5t_{3}+1)=g(1)+5t_{3}g’(1)\equiv 0(mod25)$
$5\times 41t_{3}\equiv 0(mod25)$
$41t_{3}\equiv 0(mod5)$
$t_{3}\equiv 0(mod5)$
=>$x_{3} \equiv 5t_{3}+1 \equiv 1(mod25)$

同理，
$g(5t_{4}+2)=g(2)+5t_{4}g’(2)\equiv 0(mod25)$
$135+272\times 5t_{4} \equiv 0(mod25)$
$t_{4} \equiv 4(mod 5)$
=>$x_{4} \equiv 5t_{4}+2 \equiv 22 \equiv -3(mod25)$

联立：
$\left\{\begin{matrix}
x \equiv b_{1} (mod9),b_{1}=4,5
\\
x \equiv b_{2} (mod25),b_{2}=1,-3
\end{matrix}\right.$
根据孙子定理解得：
$x \equiv 100b_{1}+126b_{2}(mod 225)$
即原式的四个解为$x \equiv 76，22，176，122(mod 225)$

例2：解同余式$f(x) \equiv 0(mod 27)$，$f(x)=x^{4}+7x+4$.
解：$f(x) \equiv 0(mod3)$，解得$x \equiv 1(mod3)$，即x=1+3t_{1}
$f’(x)=4x^{3}+7$，$f’(1)=11$，$3 \nmid 11$。

$x=1+3t_{1}$
代入$f(x) \equiv 0(mod3^{2})$
$f(1)+3t_{1}f’(1) \equiv0(mod9)$
$12+33t_{1} \equiv 0(mod9)$
$1+2t_{1} \equiv 0(mod3)$
$t_{1} \equiv 1(mod3)$
=> $t_{1}=1+3t_{2}$

$x=1+3t_{1}=1+3(1+3t_{2})=4+9t_{2}$
再代入 $f(x) \equiv 0(mod 27)$中
$288+9t_{2} \times263 \equiv 0(mod27)$
$32+263t_{2} \equiv 0(mod3)$
$2+2t_{2} \equiv 0(mod3)$
$t_{2} \equiv 2(mod3)$
=>$t_{2}=2+3t_{3}$
即$x=4+9t_{2}=4+9(2+3t_{3})=22+27t_{3}$

质数模的同余式

RSA加密原理

知识补充

欧拉函数
欧拉函数φ(a)是定义在正整数上的函数，它在正整数a上的值等于序列0，1，2…，a-1中与a互质的数的个数。

若a是质数，则φ(a)=a-1

若m1，m2是两个互质的正整数，则φ(m1m2)=φ(m1)·φ(m2)

a=p^α，p是质数，则φ(a)=( p^α ) - [ p^(α-1) ] = ( p-1 )[ p^(α-1) ]

设a=( p1^α1 )( p2^α2 )…( pk^αk )，则φ(a)=a( 1-1/p1 )( 1-1/p2 ) … ( 1-1/pk )

RSA加密

设p，q是两个大质数，例如位数超过100；N=pq；e，d满足关系：ed ≡ 1(mod φ(N))。这里密钥和解钥分别是e，N和d。加密过程如下：

设有一明码是数字a(0 ≤ a ≤ N-1)，将a通过关系a^e ≡ b(mod N)，0 ≤ b ≤ N-1，转换成b，发送方将密码b传给接收方；

接收方通过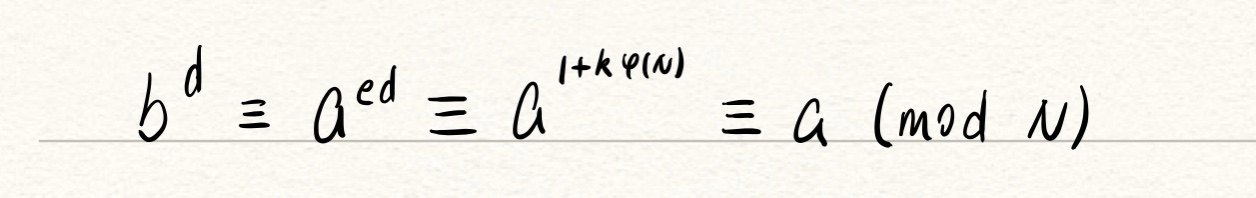

将b转换成a。φ(N)=(p-1)(q-1)

当(a，N)=1时，由欧拉定理知相等关系成立，否则需要证明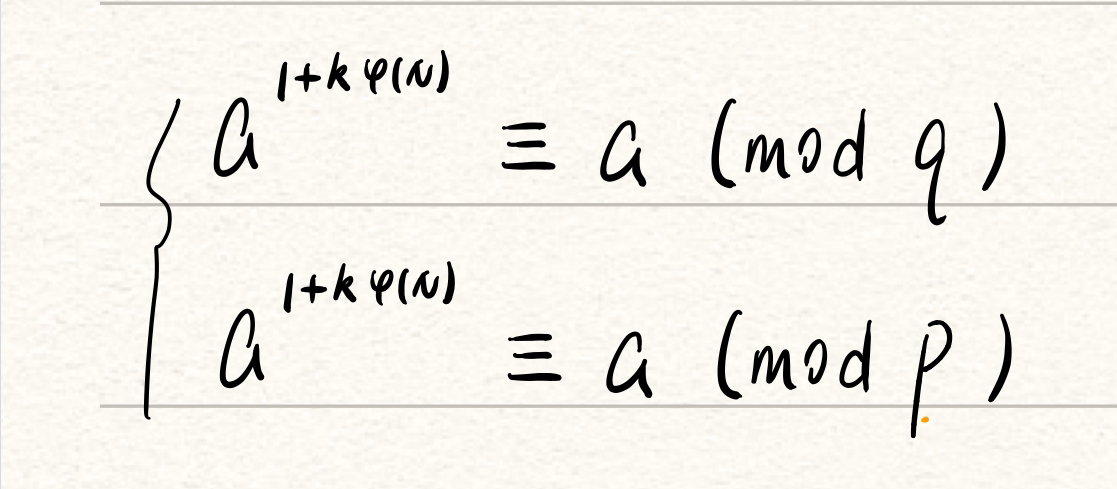

密钥e，N可以公开。要想知道d，就必须知道φ(N)，从而必须知道质因子p，q。而若p，q很大，N的分解就难以在有限时间内取得。

例子

python代码

from Crypto.Util.number import *
import gmpy2
import random
from flag import flag

p = getPrime(1024)
r = random.randint(2, 10)
e =65537
n=p**r
m=flag
assert(int(m.encode('hex'), 16) < n)
c = pow(int(m.encode('hex'), 16),e,n)
c=long_to_bytes(c)
print 'c =\n', c.encode('base64'),n


'''
c =
apxy3z3DgGnzaEedcUy3A49wAsqyyn9sqx6eYZL5iDrCq0Wjs8BOY2Ofza5wuaFigm32PVpO5jpu
Dgw9b6oX8KM2ZB9/dDmwQc7JKnAKhCQrIc1v9qt7iQbnTK0DTQj/xvQkz/IBeSjoWBmHOx4s0tDx
ZRAjOPui5wwAywNM3ynULEPczv+xN2v+6HBeoS2YuyfF5mq/pIAMPwZs+QpkuwxSbNQ6xPNP9Ox1
IeKz/41F7/D2fDsGB5CcFdAiQq+r95BhVeGzeaiQBpzwAXAPKIyO+fP6/M9XmpSJwjaMSiAUnksp
9KfVOXgEG9Z0FmxP6rgqPl0vU+rVeJ2RsTUYCSP8Vy+PD3PGwDDdUtNzvcEXKr2BKiNoOUxprBAt
yvcsmGqRLgDl1ZVgzSZ1U4MAmJ9x42mIU0XvolqaOCJZzaym1kJoBlw7/7+Nej4owEtan/c3TIkD
kr/gCenUD/8MSlvnfTUMGdQLkSht2BZiuiHxVVRVzY5ETG6v+w9AtDMC
4600616808891590817884946117009414083548013610469076381106568481948720521467073218024827360073980550620353792084520767372304347132535784875671026563160583598386773718586111034826555689602824563172463446924287072570386712719870348862904936370894695108302490867826094352072132696743116741635111860205049129717948520534270924834318704244999690532431941248905257880347561221151841978982240191397364038490250930604211256385925496658620755582058753376328583001312846508295319286941837220522563729215928111164274042890696771820759856790994461944209269732769269559257608440686713206622111649275898426040931301005711446055819707704086201357712959922814300067907536161841255533171805313149332383712997091780368142625499055149806043238057037400510197255364471685815004154357049874205884682322443391374020169114833722616851257895369648472048116320266548560787733764126281102645474252013714507014577620450816459153848279084910457288549191
'''

3*13*
11796453356132284148422938761562600214225675924279683028478380722945437234530956969294429128323092738689527969689357592743831130347384964371001958489912012357659500550437774821149419489076424374880866463705660701853957618782968842965923758029758553804789069707336180380168094605200629824934960177545822373599659300509496124689870163356274233546217714559643444924926479403669660041925945133462798197896115911135151918828684724230761295703383108946288663598655415926970307153390774138393949704878228989851570676562192222015916809796378291700732897469560166879367161203636851808270864851690464388827539561299917226173329661307550306261776146994083834852759190786838800169797734596817908360023879512966960155277428402668876957890075895456776924818141952867724500850559110593572625223410181840522260067320488593584770339437359933346415314240114658610641132163001278825791914931344702342923594079867531349150032253727426883898669649237603809250967532413494387247319852615736269410630195396174781003944827668843857879193569

283114880547174819562150530277502405141416222182712392683481137350690493628742967263066299079754225728548671272544582225851947128337239144904047003757888296583828013210506595707586067737834184997140795128935856844494982850791252231182170192714205291314937672976068329124034270524815115798439044261099736966391823212227906992556883920550581605109225149431442678198235505688071841006222683203107156749506781867243646051888433381538271096881194614710927926367729982247287371681378579321454792917077495756437696237492613328382003435113079000817589539269444005104811868887284443398500756440571145331860949471198013428159911871381207350282627527858012036466220578884131204075145630323629800640573108311207043726658281664053046989361821490962646195635406868825388020413418654245743005361844364172534241615691726246034488146496638400313967541762751806655387171912030691819005958352272856230166257916820752379600774089458245213568071581702491422023220777923865293935676462777670465855124689508194744094675864052252589100645632

分析：
getPrime(1024)返回一个随机的1024位素数p；

random.randint(2, 10)返回一个随机的满足2 ≤ r ≤ 10的数r；

公钥n等于p的r次幂（欧拉函数幂次问题）

int函数将明文信息（设为a）转化为16进制整型，pow函数先取幂再取模，即a^e ≡ c (mod n)

再利用long_to_bytes函数把长整数转换为字节字符串，再base64加密一下。

得到c和n。

所以解密思路是：

分解n，得到n等于某个质数p的r次方。

base64解码c，再bytes_to_long转化加密信息c。

利用欧拉函数求φ(n)，由于是幂次问题，可以通过φ(n)=( p-1 )[ p^(r-1) ]求得φ(n)。

因为ed ≡ 1(mod φ(N))，所以d是e关于φ(N)的逆模，利用libnum.modular.invmod函数求逆模，找出d；

要求明文信息a，因为（c^d） ≡ a （mod n），所以c的d次方取模n就是明文a,再转化成字符串得到flag。

python代码：

import libnum
from Crypto.Util.number import *
import gmpy2
import random
import base64

n=4600616808891590817884946117009414083548013610469076381106568481948720521467073218024827360073980550620353792084520767372304347132535784875671026563160583598386773718586111034826555689602824563172463446924287072570386712719870348862904936370894695108302490867826094352072132696743116741635111860205049129717948520534270924834318704244999690532431941248905257880347561221151841978982240191397364038490250930604211256385925496658620755582058753376328583001312846508295319286941837220522563729215928111164274042890696771820759856790994461944209269732769269559257608440686713206622111649275898426040931301005711446055819707704086201357712959922814300067907536161841255533171805313149332383712997091780368142625499055149806043238057037400510197255364471685815004154357049874205884682322443391374020169114833722616851257895369648472048116320266548560787733764126281102645474252013714507014577620450816459153848279084910457288549191
c='apxy3z3DgGnzaEedcUy3A49wAsqyyn9sqx6eYZL5iDrCq0Wjs8BOY2Ofza5wuaFigm32PVpO5jpuDgw9b6oX8KM2ZB9/dDmwQc7JKnAKhCQrIc1v9qt7iQbnTK0DTQj/xvQkz/IBeSjoWBmHOx4s0tDxZRAjOPui5wwAywNM3ynULEPczv+xN2v+6HBeoS2YuyfF5mq/pIAMPwZs+QpkuwxSbNQ6xPNP9Ox1IeKz/41F7/D2fDsGB5CcFdAiQq+r95BhVeGzeaiQBpzwAXAPKIyO+fP6/M9XmpSJwjaMSiAUnksp9KfVOXgEG9Z0FmxP6rgqPl0vU+rVeJ2RsTUYCSP8Vy+PD3PGwDDdUtNzvcEXKr2BKiNoOUxprBAtyvcsmGqRLgDl1ZVgzSZ1U4MAmJ9x42mIU0XvolqaOCJZzaym1kJoBlw7/7+Nej4owEtan/c3TIkDkr/gCenUD/8MSlvnfTUMGdQLkSht2BZiuiHxVVRVzY5ETG6v+w9AtDMC'
yz=libnum.factorize(n)
cf=bytes_to_long(base64.b64decode(c))
#print(cf)
#print(yz)
for k,v in yz.items():
	p=k;
	r=v;
phi=(p**(r-1))*(p-1)
e=65537
d = libnum.modular.invmod(e, phi)
m = libnum.n2s(pow(cf, d, n)) 
print(m)