在R²={(a,b)|a,b∈R}中,规定加法和乘法运算:
(a, b)+(c, d) = (a+c, b+d) R²在这个规定下构成一个加法交换群。
(a, b)(c, d) = (ac-bd, ad+bc) R²去掉(0, 0)在这个规定下构成一个乘法交换群。
易验证它构成一个域。将规定了上述加法和惩罚后的R²用C表示,称为复数域。
易看出{(a,0)|a∈R}构成C的一个子域,与实数域R同构。
R的单位元素是1,通常将(1, 0)简记为1,称为C的单位元素。
另外还有一个元素(0, 1),将其简记为i,称其为虚数单位。
可见,按照上面规定过的乘法运算法则,i²=(-1, 0)= -(1, 0) = -1。
C中的元素(a, b)可简记为a+ib。
再进一步,负数中规定的乘法运算,本质上是“想象出”一个i,满足i² = -1,然后按照分配律展开,再按照交换律合并同类项。
可是这个想象的合理性如何论证?
复数乘法定义和i² = -1的合理性
考虑二阶方阵(涉及矩阵了,我不会打,手写吧)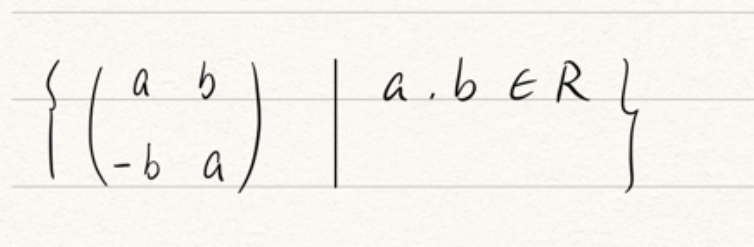
矩阵的加法和乘法运算都是十分合理的。在线性变换(可看作映射)中,两个线性变换可以进行加法运算,即两个映射作用于同一空间,两个映射可以进行加法运算。若第一个映射映过去的像空间是第二个映射的定义域,两个映射还可以进行复合运算。于是自然产生了乘法运算。
上述矩阵在矩阵的加法和乘法运算: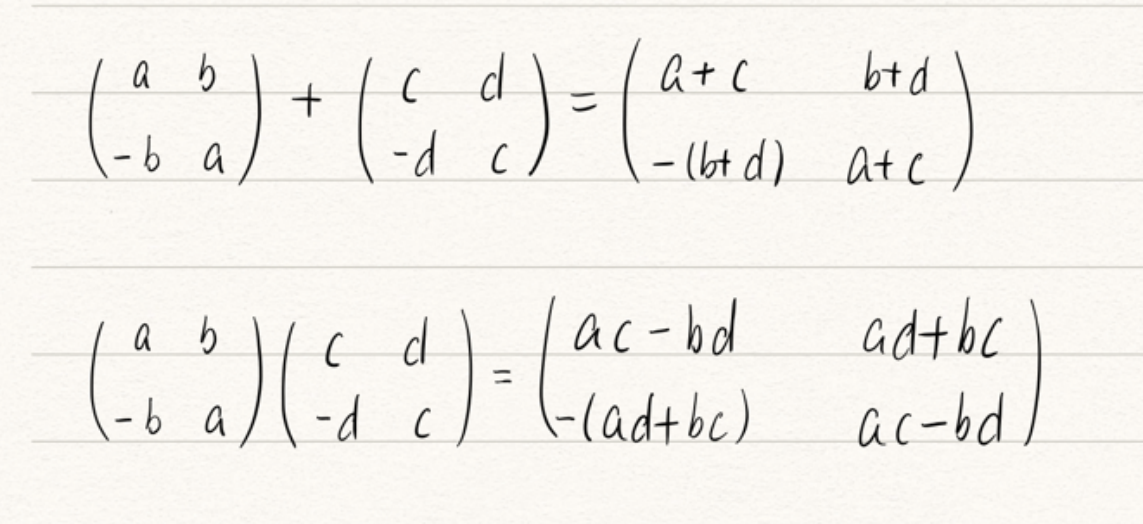
下也构成了域。显然与复数域同构。
这就说明,复数的乘法本质上就是矩阵的乘法。
那么(1, 0)与(0, 1)是什么?
这个矩阵,很明显可以看出,是将行向量逆时针旋转π/2。如下:
即,作线性变换,将二位行向量逆时针旋转π/2。其平方
将二位行向量逆时针旋转π,即乘了-1。这就说明了i² = -1的几何意义的合理性。